Question

At equilibrium, the concentrations of reactants and products can be predicted using the equilibrium constant, Kc, which is a mathematical expression based on the chemical equation. For example, in the reaction aA+bB⇌cC+dD where a, b, c, and d are the stoichiometric coefficients, the equilibrium constant is Kc=[C]c[D]d[A]a[B]b where [A], [B], [C], and [D] are the equilibrium concentrations. If the reaction is not at equilibrium, the quantity can still be calculated, but it is called the reaction quotient, Qc, instead of the equilibrium constant, Kc. Qc=[C]tc[D]td[A]ta[B]tb where each concentration is measured at some arbitrary time t. Part A A mixture initially contains A, B, and C in the following concentrations: [A] = 0.350 M , [B] = 0.800 M , and [C] = 0.500 M . The following reaction occurs and equilibrium is established: A+2B⇌C At equilibrium, [A] = 0.150 M and [C] = 0.700 M . Calculate the value of the equilibrium constant, Kc. Express your answer numerically.

Answer 1

Answer: The value of equilibrium constant for the above reaction is 12.7

Step-by-step explanation:

Equilibrium constant in terms of concentration is defined as the ratio of concentration of products to the concentration of reactants each raised to the power their stoichiometric ratios. It is expressed as
`K_(c)`

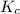
For a general chemical reaction:

`aA+bB\rightleftharpoons cC+dD`

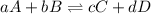
The expression for
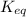`K_(eq)` is written as:

`K_(eq)=([C]^c[D]^d)/([A]^a[B]^b)`

For the given chemical reaction:

`A+2B\rightleftharpoons C`

Initial: 0.350 0.800 0.500

At Eqllm: 0.350-x 0.800-x 0.500+x

We are given:

`[A]_(eq)=0.150M`

`[C]_(eq)=0.700M`

Calculating for 'x'. we get:

`0.500+x=0.700\\\\x=0.200`

So, the equilibrium concentration of B will be

`[B]_(eq)=(0.800-x)=0.800-0.200=0.600M`

The expression of
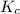`K_(c)` for above reaction follows:

`K_c=([C])/([A][B]^2)`

Putting values in above equation, we get:

`K_c=(0.700)/(0.150* (0.600)^2)\\\\K_c=12.7`

Hence, the value of equilibrium constant for the above reaction is 12.7