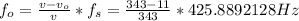A street musician sounds the A string of his violin, producing a tone of 440 Hz, What frequency does a bicyclist hear as he a) approaches and b) recedes from the musician with a…

Question

asked Dec 10, 2020 42.4k views

1 Answer

Calzzetta · Answer 1 · 2020-12-15T22:52:21+0000

Answer:

a)
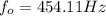
f_o=454.11Hz

b)
f_o=425.89Hz

Step-by-step explanation:

Let´s use Doppler effect, in order to calculate the observed frequency by the byciclist. The Doppler effect equation for a general case is given by:

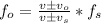
$f_o=(v\pm v_o)/(v\pm v_s) *f_s$

where:

$f_o=Observed\hspace{3}frequency$

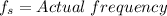
$f_s=Actual\hspace{3}frequency$

$v=Speed\hspace{3}of\hspace{3}the\hspace{3}sound\hspace{3}waves$

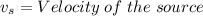
$v_s=Velocity\hspace{3}of\hspace{3}the\hspace{3}source$

$v_o=Velocity\hspace{3}of\hspace{3}the\hspace{3}observer$

Now let's consider the next cases:

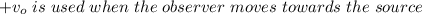
$+v_o\hspace{3}is\hspace{3}used\hspace{3}when\hspace{3}the\hspace{3}observer\hspace{3}moves\hspace{3}towards\hspace{3}the\hspace{3}source$

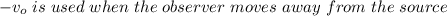
$-v_o\hspace{3}is\hspace{3}used\hspace{3}when\hspace{3}the\hspace{3}observer\hspace{3}moves\hspace{3}away\hspace{3}from\hspace{3}the\hspace{3}source$

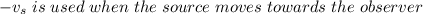
$-v_s\hspace{3}is\hspace{3}used\hspace{3}when\hspace{3}the\hspace{3}source\hspace{3}moves\hspace{3}towards\hspace{3}the\hspace{3}observer$

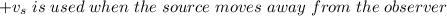
$+v_s\hspace{3}is\hspace{3}used\hspace{3}when\hspace{3}the\hspace{3}source\hspace{3}moves\hspace{3}away\hspace{3}from\hspace{3}the\hspace{3}observer$

The data provided by the problem is:

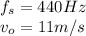
$f_s=440Hz\\v_o=11m/s$

The problem don't give us aditional information about the medium, so let's assume the medium is the air, so the speed of sound in air is:

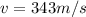
v=343m/s

Now, in the first case the observer alone is in motion towards to the source, hence:

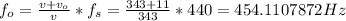
f_o=(v+v_o)/(v)*f_s=(343+11)/(343) *440=454.1107872Hz

Finally, in the second case the observer alone is in motion away from the source, so:

f_o=(v-v_o)/(v)*f_s=(343-11)/(343) *425.8892128Hz