Question

A strong gust of wind blows an apple off a tree. The apple has a mass of 0.25 kg. The gust of wind pushes the apple with a force of 1.05 N to the right. What is the net force on the apple?

5.5 N
- 2.2 N
1.78 N
2.66 N

Answer 1

2.66N

Step-by-step explanation:

Answer 2

For this case we must draw the free body diagram of the apple.

It is observed in the attached figure that we have the force of the wind acting to the right, in addition to the force of the weight that goes down.

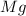`Mg`: It is the force exerted by the weight of the apple (M: It is the mass and g: It is the acceleration of gravity)

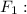`F_ {1}:` It is the force exerted by the wind

Then, the net force will be given by:

`F_ {n} = \sqrt {(Mg) ^ 2 + (F_ {1}) ^ 2}`

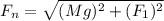
We have to:

`Mg = 0.25kg * 9.8 \frac {m} {s ^ 2} = 2.45N\\F_ {1} = 1.05N`

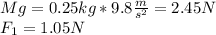
Substituting we have:

`F_ {n} = \sqrt {(2.45) ^ 2 + (1.05) ^ 2}\\F_ {n} = \sqrt {6.0025 + 1.1025}\\F_ {n} = \sqrt {7.105}\\F_ {n} = 2.66`

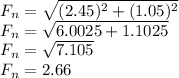
Thus, the net force acting on the apple is 2.66N

Answer:

Option D