Question

A hammer weighs 11 N on the surface of the earth. What is the weight of this hammer on the surface of a planet with a mass 3 x 10^18 Kg and a radius of 4.21 x 10^4 m ?

Answer 1

The weight is 0.121 N

Step-by-step explanation:

The weight (W) is defined by:

W=mg (I)

where m is the mass and g is the acceleration of gravity

You have to calculate the mass of the hammer and then the acceleration of gravity on the given planet, in order to calculate the weight of the hammer in that planet

Dividing (I) by g:

m=W/g

g on earth = 9.8 m/s²

Calculating the mass of the hammer:

m=11/9.8=1.1 kg

Now, you have to calculate the acceleration of gravity on the other planet, which is given by:

`g=G(M)/(R^(2) )`

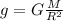
where G is the universal gravitational constant , M is the mass of the planet, and R is the radius of the planet.

Is known that G= 6.67 x
`10^(-11)` N m²/kg²

Calculating the value of g:

g =
`(6.67)(10^(-11)) ((3)(10^(18)) )/([(4.21)(10^(4))] ^(2) )`

g= 0.11 m/s²

So the weight in that planet (Wp) is:

Wp=(1.1)(0.11) = 0.121 N