Question

What are the solutions to the equation? x^3 - 8x^2 - x + 8 =0

Answer 1

Explanation:

x^3 - 8x² - x + 8 =0

x^3 - 8x² - (x - 8 )=0

x²(x-8) - (x-8) = 0

(x-8)(x² -1) =0

x-8 = 0 or x² - 1 = 0

x-8=0 or (x-1)(x+1)=0

x=8 x=1 or x=-1

Answer 2

The solutions of the
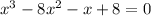`x^(3)-8 x^(2)-x+8=0` is -1, 1, 8

SOLUTION:

Given, cubic equation is
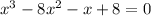`x^(3)-8 x^(2)-x+8=0` --- eqn 1

We need to find the solutions of the given cubic equation.

When we observe the equation clearly, we can notice that sum of coefficients is zero

According to polynomial identities, we can say that 1 is one of its solutions.

Let, a,b,c be the solutions of any equation, then its general form is

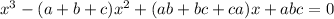`x^(3)-(a+b+c) x^(2)+(a b+b c+c a) x+a b c=0` --- eqn (2)

On comparing both (1) and (2)

a + b + c = 8, ab +bc + ca = -1, abc = -8

We know, one solution is 1, let it be c, i.e. c=1

a + b + 1 = 8, ab + b +a = -1, ab = -8

We can conclude that a + b = 7, ab = -8, from above three equations

We know that,
`(a-b)^(2)=(a+b)^(2)-4 a b`

`(a-b)^(2)=7^(2)-4 *(-8)`

`(a-b)^(2)=49+32`

`(a-b)^(2)=81`

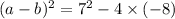
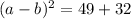
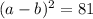
(a-b)=9

add (a + b) and (a – b) we get

a+ b + a-b = 7 + 9

2a = 16

a = 8

Substitute a value in a+b =7 , we get

8 + b =7

b =-1

Hence, the solutions of the
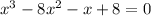`x^(3)-8 x^(2)-x+8=0` is -1 , 1 , 8