Answer:
After 4.5 seconds the ball reaches ground.
Explanation:
We equation of motion given as y = -16t²-18t+405,
We need to find in how many seconds will the ball hit the ground,
That is we need to find time when y = 0
0 = -16t²-18t+405
16t²+18t-405 = 0
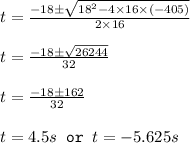
Negative time is not possible, hence after 4.5 seconds the ball reaches ground.