ANSWER:
Width of border is 1.5 inches
SOLUTION:
Given,
Width of the photo graph
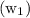 = 4.25 inches
= 4.25 inches
Height of the photo graph
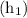 = 7.75 inches
= 7.75 inches
And it is mounted in a frame with border of x inches, so the dimensions after mounting will be
Width after mounting
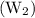 = (4.25 + x + x) [ since, two sides of photograph will have borders
= (4.25 + x + x) [ since, two sides of photograph will have borders
Height after mounting
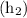 = (7.75 + x + x) [ since, two sides of photograph will have borders
= (7.75 + x + x) [ since, two sides of photograph will have borders
Area of border = 45 square inches
As we all know that, photograph will be in rectangular shape,
Area of photograph =
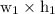
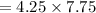
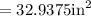
Area of photograph after mounting =
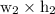
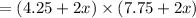
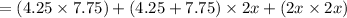
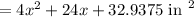
Now, area of border = Area of photograph after mounting - Area of photograph before mounting
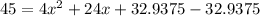
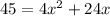
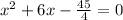 [by dividing the equation with 4]
[by dividing the equation with 4]
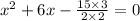
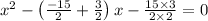
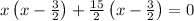
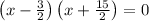
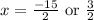
As length can’t be negative, x =
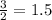
Hence , the width x is 1.5 inches