Question

A picture is 4.25 inches wide and 7.75 inches tall. It is mounted in a frame with a border of x inches wide on all sides. If the area of the shaded border is 45 inches squared, what is its width x?

Answer 1

Width of border is 1.5 inches

SOLUTION:

Given,

Width of the photo graph
`\left(\mathrm{w}_(1)\right)` = 4.25 inches

Height of the photo graph
`\left(\mathrm{h}_(1)\right)` = 7.75 inches

And it is mounted in a frame with border of x inches, so the dimensions after mounting will be

Width after mounting
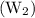`\left(\mathrm{W}_(2)\right)` = (4.25 + x + x) [ since, two sides of photograph will have borders

Height after mounting
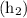`\left(\mathrm{h}_(2)\right)` = (7.75 + x + x) [ since, two sides of photograph will have borders

Area of border = 45 square inches

As we all know that, photograph will be in rectangular shape,

Area of photograph =
`\mathrm{w}_(1) * \mathrm{h}_(1)`

`= 4.25 * 7.75`

`=32.9375 \mathrm{in}^(2)`

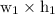
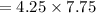
Area of photograph after mounting =
`\mathrm{w}_(2) * \mathrm{h}_(2)`

`= (4.25+2x) * (7.75+2x)`

`= (4.25 * 7.75) + (4.25 + 7.75) * 2x + (2x * 2x)`

`=4 x^(2)+24 x+32.9375 \text { in }^(2)`

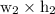
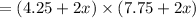
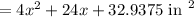
Now, area of border = Area of photograph after mounting - Area of photograph before mounting

`45=4 x^(2)+24 x+32.9375-32.9375`

`45=4 x^(2)+24 x`

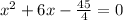`x^(2)+6 x-(45)/(4)=0` [by dividing the equation with 4]

`x^(2)+6 x-(15 * 3)/(2 * 2)=0`

`x^(2)-\left((-15)/(2)+(3)/(2)\right) x-(15 * 3)/(2 * 2)=0`

`x\left(x-(3)/(2)\right)+(15)/(2)\left(x-(3)/(2)\right)=0`

`\left(x-(3)/(2)\right)\left(x+(15)/(2)\right)=0`

`x=(-15)/(2) \text { or } (3)/(2)`

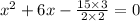
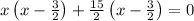
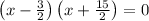
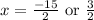
As length can’t be negative, x =
`(3)/(2) = 1.5`

Hence , the width x is 1.5 inches