Question

A population of bacteria is introduced into a culture. The number of bacteria P can be modeled by P(t) = 800 1 + 9t 90 + t2 , where t is the time in hours since the bacteria was introduced. Find the rate of change of the population (in bacteria per hour) after 6 hours. (Round your answer to one decimal place.)

Answer 1

Answer: Hello mate!

you know that the equation is (or at least i think this is):

p(t) = 800 + 9t/90 + t^2

You want to know the "rate of change" after 6 hours.

We know that the rate of change is the derivative of P(t) with respect to t; this is

`(dP(t))/(dt) = 9/90 + 2t`

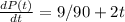
now we want the rate of change when t = 6, then we replace t by 6 in the derivate equation:

`p(6)' = 0.9 + 2*6 = 12.9`

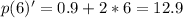
so the rate of change after 6 hours is 12.9

where
`P'(t) = (dP(t))/(dt)`

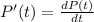
If the equation is wrong ( because you write P(t) = 800 1 + 9t 90 + t2, and i don really know how to iterprete it) tellme and we can do the derivate again :D