Question

Batteries produced by a manufacturing company have had a life expectancy of 135 hours. Because of an improved production process, the company believes that there has been anincreasein the life expectancy of its batteries. A sample of 42 batteries showed an average life of 140 hours. From past information, the standard deviation of the population is known to be 24 hours. a.Start by writing down the null and alternative hypotheses.b.Next, calculatethe relevant test statistic.c.What conclusion can be made at the .10 level of significance? Make sure to interpret in words.

Answer 1

Answer with explanation:

Let
`\mu` represents the population mean .

By considering the given information, we have

a)

`\text{Null hypothesis }H_0: \mu\leq135\\\\\text{Alternative hypothesis }H_a: \mu>135`

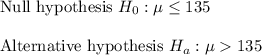
Since the alternative hypothesis is right-tailed , so the test is right-tailed test.

Given : n= 42 > 30 , so we use z-test.

`\overline{x}=140` ;
`\sigma=24`

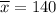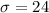
Test statistic :
`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

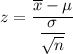
i.e.
`z=(140-135)/((24)/(√(42)))\approx1.35`

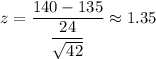
P-value (right tailed test)=
`P(Z>1.35)=1-P(z<1.35)=1-0.911492=0.088508`

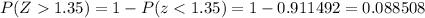
Since , the p-value (0.088508) is less than the significance level,thus we reject the null hypothesis .

Conclusion : We have sufficient evidence to support the claim that Because of an improved production process, the company believes that there has been an increase in the life expectancy of its batteries.