Question

The state of Virginia has implemented a Standard of Learning (SOL) test that all public school students must pass before they can graduate from high school. A passing grade is 75. Montgomery County High School administrators want to gauge how well their students might do on the SOL test, but they don’t want to take the time to test the whole student population. Instead, they selected 20 students at random and gave them the test. The results are as follows: 83 79 56 93 48 92 37 45 72 71 92 71 66 83 81 80 58 95 67 78 Assume that SOL test scores are normally distributed. a. Compute the mean and standard deviation for these data. b. Determine the probability that a student at the high school will pass the test. c. How many percent of students will receive a score between 75 and 95? d. What score will put a student in the bottom 15% in SOL score among all students who take the test? e. What score will put a student in the top 2% in SOL score among all students who take the test? g

Answer 1

a. Mean = 72.35

Standard deviation = 16.68

Mean =
`\frac{\text{Sum of all the observation}}{\text{Total number of observtions}}`

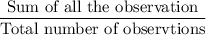
and,
`Standard deviation(\sigma) = \sqrt{(1)/(n)\sum_(i=1)^(n){(x_(i)-\bar{x})^(2)} }`

where,
`\bar{x}` is mean of the distribution.

b. The passing grade is 75.

The students whose grade is less than 75 are fail

There are 10 students whose grade are more than 75.

Thus, Probability of pass students = 10 ÷ 20 = 0.5

c. There are 10 students that score between 75 and 95.

∴ Probability = 10 ÷ 20 = 0.5

d. The 15% of 20 = 3 students.

Thus the score will put a student in the bottom 15% = 48

e. Thus, the score will put a student in the top 2% = 95