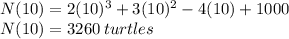Answer:
The turtle population's rate of growth will be 32 turtles per year after 2 years and 248 per year after 6 years.
Ten years after the conservation measures are implemented the population will be 3260 turtles.
Explanation:
To find the rate of growth of the turtle population at any time t you need to find
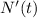
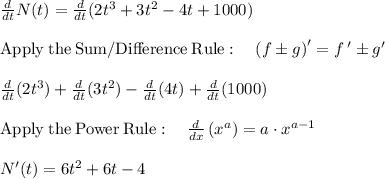
In particular, when t = 2 and t = 6, we have

so the turtle population's rate of growth will be 32 turtles per year after 2 years and 248 per year after 6 years.
The turtle population at the end of the tenth year will be