Answer:
The initial population is 6598.
Explanation:
Given : The population of a community is known to increase at a rate proportional to the number of people present at time t. The initial population
 has doubled in 5 years. Suppose it is known that the population is 10,000 after 3 years.
has doubled in 5 years. Suppose it is known that the population is 10,000 after 3 years.
To find : What was the initial population
 ?
?
Solution :
Using the formula,
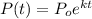
The initial population
 has doubled in 5 years.
has doubled in 5 years.
i.e.
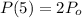
For t=5,
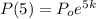
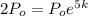
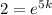
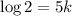
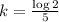
Substitute in the equation,
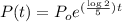
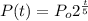
Substitute, P(t)=10,000 and t=3 years
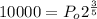
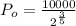
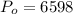
Therefore, The initial population is 6598.