Answer:
The probability that the dogs are blue eyed and deaf is 13.02%.
Explanation:
We are given the following information in the question:
P(Blue eyes) = 31%
P(Deaf) = 38%
P(Deaf | Blue eyes) = 42%
Formula for conditional probability:
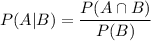
Now, let A be the event where the dog is deaf and B be the the event where dog is blue eyed.

Hence, the probability that the dogs are blue eyed and deaf is 13.02%.