Question

The matrix below represents a system of equations

2 -3 1-2
2 2 42
Which of the following describes the solution to this system of equations?
dependent
inconsistent
independent
unique

Answer 1

dependent its on apex.

Answer 2

Independent.

Explanation:

To know the type of the given system, we need to solve it.

The given system of equations is

`\left \{ {{2x-31y=-2} \atop {2x+2y=42}} \right.`

We can solve this system by multiplying the first equation with -1, and subtracting after

`\left \{ {{-2x+31y=+2} \atop {2x+2y=42}} \right.\\\\33y=44\\y=(44)/(33)\\ y=(4)/(3)`

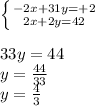
Then, we use this value to find the other one

`2x+2y=42\\2x+2(4)/(3)=42\\ 2x=42-(8)/(3)\\ 2x=(126-8)/(3) \\2x=(118)/(3) \\x=(118)/(6)\\ x=(59)/(3)`

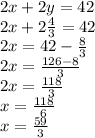
As you observe, the system has a solution, which is
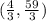`((4)/(3), (59)/(3))`. That means the system cannot be inconsistent. because it has a solution. Remember that inconsitent systems refer to those that don't have any solution, that is, the lines are parallel.

On the other hand, independent systems are those where each equation produces a different line, and the solution is the interception of those lines, like this case. We have a solution and two different lines represented by each linear equation.

Therefore, the right answer is independent.