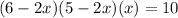Question

You have a rectangular piece of cardboard that is 6 feet long and 5 feet wide. You want to make a box, so you cut out squares

of length x at each of the comers. You then fold the sides up to make a box with no top. If the volume of the box is 10 ft,
what was the size of the square you cut off of the corners?
Write an equation that you would use to solve for x, the edges of the squares
A
30x = 10
3
B.XX-6)(x - 5) = 10
C.X(6-X)/5 - x) = 10
D.x[5 - 2X)/5 - 2x) = 10

Answer 1

`(6-2x)(5-2x)(x)=10`

Explanation:

see the attached figure to better understand the problem

Let

x -----> the edges of the squares in feet

we know that

The volume of the box is equal to

`V=LWH`

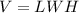
we have

`L=(6-2x)\ ft\\W=(5-2x)\ ft\\H=x\ ft`

`V=10\ ft^3`

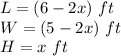
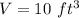
substitute and solve for x

`10=(6-2x)(5-2x)(x)\\10=(30-12x-10x+4x^(2))(x)\\10=(30x-22x^2+4x^(3))\\4x^(3)-22x^(2) +30x-10=0`

therefore

The equation that you would use to solve for x is

`(6-2x)(5-2x)(x)=10`