Question

Is there a real number x such that x 4 + x = 3? If your answer is no, justify why no such x exists. If your answer is yes, justify why at least one solution to x 4 + x = 3 exists, and find an interval (a, b) (where a, b are real numbers) which is guaranteed to contain such an x.

Answer 1

Answer: Hello mate!

Our equation is
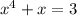`x^(4) + x = 3` and we want to know if this equation has a solution.

Now, our equation is clearly a continuous and differentiable equation, then it passes throw all the positive values y where y(x) = x^4 + x

then there should be at least a value of x where y takes the value of 3. Let's try to find the interval (a,b) where this number x lives.

y(1) = 1^4 + 1 = 2, then we could take 1 as the lower limit a.

y(2) = 16 + 2 = 18, then we could take 2 as the upper limit b.

And because Y is continuos and only increases when x is positive, then betwen x = 1 and x= 2, y(x) passes trhough all the values between y = 2 and y = 18.

then we could assure that there is a solution in (1,2)

but there are more!

y(-1) = 0, then we could take b = -1

and y(-2) = 16 - 2 = 14, then we could take a = -2

then in the interval (-2. -1) there is other solution if we use the same reasoning as before,