Question

Prove that for every pair of integers m and n, if n − m is even, then n 2 − m is also even. (You may freely use the fact that the sum of two odd numbers is even, that the sum of an odd number and an even number is odd, the product of an odd and an even is even, etc.)

Answer 1

Answer with Step-by-step explanation:

We are given that n and m are two integers

We have to prove that if n-m is even , then
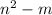`n^2-m` is also even.

We know that sum of two odd numbers is even.Sum of an odd number and even number is odd.

Product of an odd number and even number is even.

Case 1.Suppose m and n are both even n=4 , m=2

`4-2=2`

`(4)^2-2=14 =Even`

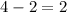
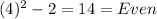
Case 2.Suppose m odd and n odd

n=9,m=5

`9-5=4`

`(9)^2-5=76=Even`

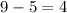
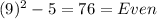
Hence, proved.