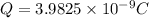Question

A parallel-plate capacitor with plates of area 360 cm2 is charged to a potential difference V and is then disconnected from the voltage source. When the plates are moved 0.8 cm farther apart, the voltage between the plates increases by 100 V. What is the charge Q on the positive plate of the capacitor?

Answer 1

`Q=3.9825* 10^(-9) C`

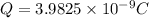
Step-by-step explanation:

We are given that a parallel- plate capacitor is charged to a potential difference V and then disconnected from the voltage source.

1 m =100 cm

Surface area =S=
`(360)/(10000)=0.036 m^2`

`\Delta d=0.8 cm=0.008 m`

`\Delta V=100 V`

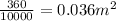
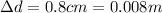
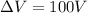
We have to find the charge Q on the positive plates of the capacitor.

V=Initial voltage between plates

d=Initial distance between plates

Initial Capacitance of capacitor

`C=(\epsilon_0 S)/(d)`

Capacitance of capacitor after moving plates

`C_1=(\epsilon_0 S)/((d+\Delta d))`

`V=(Q)/(C)`

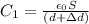
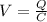
Potential difference between plates after moving

`V=(Q)/(C_1)`

`V+\Delta V=(Q)/(C_1)`

`(Qd)/(\epsilon_0S)+100=(Q(d+\Delta d))/(\epsilon_0S)`

`(Q(d+\Delta d))/(\epsilon_0 S)-(Qd)/(\epsilon_0S)=100`

`(Q\Delta d)/(\epsilon_0 S)=100`

`\epsilon_0=8.85* 10^(-12)`

`Q=(100* 8.85* 10^(-12)* 0.036)/(0.008)`

`Q=3.9825* 10^(-9) C`

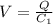
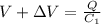
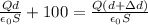
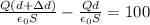
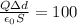
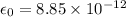
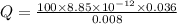
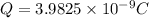
Hence, the charge on positive plate of capacitor=
`Q=3.9825* 10^(-9) C`