Question

1. Nemo deposits $7000 now, $6000 three years from now, and $1500 six years from now into a fund paying 8% compounded quarterly: What equal deposit of size A, made every 3 months (with the first deposit at t=0 and last deposit at the end of the 7th year) are equal to the 3 deposits?

Answer 1

A quota of $ 583.388 every thre months is equivalent to these three deposits.

Step-by-step explanation:

We need to first calculate the future value of the deposits

and then, we calculate the PMT which is equivalent

`Principal \: (1+ r)^(time) = Amount`

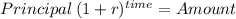
First deposit:

Principal $ 7,000

time 28 (7 years x 4 quarter per year)

rate 0.02 (8% over 4 = 2% quarterly)

`7000 \: (1+ 0.02)^(28) = Amount`

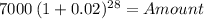
Amount 12,187.17

Second deposit:

`6000 \: (1+ 0.02)^(16) = Amount`

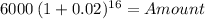
Amount 8,236.71

Third deposit:

`1500 \: (1+ 0.02)^(4) = Amount`

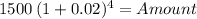
Amount 1,623.65

Total: 12,187.17 + 8,236.71 + 1,623.65 = 22,047.53‬

Now we solve for a PMT annuity-due (we are doing the first deposit at the beginning of the period)

`PV / ((1+r)^(time) -1)/(rate)(1+r) = C\\`

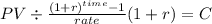
FV $22,047.53

time 28 (7 years 4 quar a year)

rate 0.02 (8% per year divide into 4 = 2% quarterly)

`22047.53 / ((1+0.02)^(28) + 1 )/(0.02)(1.02) = C\\`

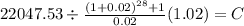
C $ 583.388