Question

a) If we assume that the population of Goomba heights is normally distributed with mean 12 inches andstandard deviation 6 inches, what is the probability that a randomly chosen Goomba has a height between 13 and 15 inches? (b) Koopa Troopas, another enemy of Mario & Luigi, have normally distributed heights, with mean 15 inches and standard deviation 3 inches. What is the probability that a randomly selected KoopaTroopa is taller than the shortest 75% of Goombas? (Hint: First compute the height such that75% of Goombas are shorter than that height. Then compute the probability that a KoopaTroopa is taller than that height.) (c) What is the probability that a randomly selected Goomba is taller than the shortest 75% of KoopaTroopas?

Answer 1

a) 12.40% probability that a randomly chosen Goomba has a height between 13 and 15 inches

b) 36.32% probability that a randomly selected KoopaTroopa is taller than the shortest 75% of Goombas

c) 20.05% probability that a randomly selected Goomba is taller than the shortest 75% of KoopaTroopas

Explanation:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

a) If we assume that the population of Goomba heights is normally distributed with mean 12 inches and standard deviation 6 inches, what is the probability that a randomly chosen Goomba has a height between 13 and 15 inches?

We have that
`\mu = 12, \sigma = 6`

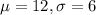
This probability is the pvalue of Z when X = 15 subtracted by the pvalue of Z when X = 13. So

X = 15

`Z = (X - \mu)/(\sigma)`

`Z = (15 - 12)/(6)`

`Z = 0.5`

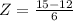
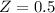
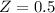`Z = 0.5` has a pvalue of 0.6915.

X = 13

`Z = (X - \mu)/(\sigma)`

`Z = (13 - 12)/(6)`

`Z = 0.17`

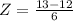
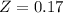
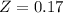`Z = 0.17` has a pvalue of 0.5675

0.6915 - 0.5675 = 0.124

12.40% probability that a randomly chosen Goomba has a height between 13 and 15 inches

(b) Koopa Troopas, another enemy of Mario & Luigi, have normally distributed heights, with mean 15 inches and standard deviation 3 inches. What is the probability that a randomly selected KoopaTroopa is taller than the shortest 75% of Goombas? (Hint: First compute the height such that75% of Goombas are shorter than that height. Then compute the probability that a KoopaTroopa is taller than that height.)

Shortest 75% of Goombas.

75th percentile of Goombas, which is X when Z has a pvaue of 0.75. So it is X when = 0.675.

`Z = (X - \mu)/(\sigma)`

`0.675 = (X - 12)/(6)`

`X - 12 = 6*0.675`

`X = 16.05`

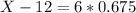
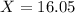
For Koopa Troopas,
`\mu = 15, \sigma = 3`

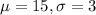
This probability is 1 subtracted by the pvalue of Z when X = 16.05.

`Z = (X - \mu)/(\sigma)`

`Z = (16.05 - 15)/(3)`

`Z = 0.35`

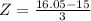
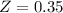
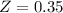`Z = 0.35` has a pvalue of 0.6368

1 - 0.6368 = 0.3632

36.32% probability that a randomly selected KoopaTroopa is taller than the shortest 75% of Goombas

(c) What is the probability that a randomly selected Goomba is taller than the shortest 75% of KoopaTroopas?

75th percentile of Koopa Troopas.

`Z = (X - \mu)/(\sigma)`

`0.675 = (X - 15)/(3)`

`X - 15 = 3*0.675`

`X = 17.025`

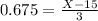
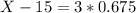
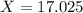
This probability is 1 subtracted by the pvalue of Z when X = 17.025. So

`Z = (X - \mu)/(\sigma)`

`Z = (17.025 - 12)/(6)`

`Z = 0.84`

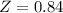
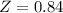`Z = 0.84` has a pvalue of 0.7995

1 - 0.7995 = 0.2005

20.05% probability that a randomly selected Goomba is taller than the shortest 75% of KoopaTroopas

Answer 2

`\mu = 12\\\sigma = 6`

a) what is the probability that a randomly chosen Goomba has a height between 13 and 15 inches?

Formula :
`z=(x-\mu)/(\sigma)`

`z=(13-12)/(6)\\z=0.1666`

refer the z table

P(z<0.166)=0.5636

`z=(15-12)/(6)`

z=0.5

refer the z table

P(z<0.5)=0.6554

P(13<x<15)=P(0.166<z<0.5)=P(z<0.5)-P(z<0.166)= 0.6554-0.5636=0.0918

Hence he probability that a randomly chosen Goomba has a height between 13 and 15 inches is 0.0918

b) Koopa Troopas, another enemy of Mario & Luigi, have normally distributed heights, with mean 15 inches and standard deviation 3 inches. What is the probability that a randomly selected KoopaTroopa is taller than the shortest 75% of Goombas

`\mu = 15\\\sigma = 3`

P(shortest)=0.75

P(tallest)=1-0.75= 0.25

Hence the probability that a randomly selected KoopaTroopa is taller than the shortest 75% of Goombas is 0.25

c) What is the probability that a randomly selected Goomba is taller than the shortest 75% of KoopaTroopas?

The probability that a randomly selected KoopaTroopa is taller than the shortest 75% of Goombas is 0.25