Question

PLEASE HELP ASAP!!
Rewrite the expression with a rational exponent as a radical expression.

Answer 1

D)- 3√5^4

Your answer is D^

Answer 2

`5^{(1)/(2) } =√(5)`

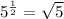
Explanation:

Here we need to use the following property

`x^{(a)/(b) }=\sqrt[b]{x^(a) }`

So, we use this property to rewrite the given expression

`(5^{(3)/(4) } )^{(2)/(3) }`

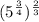
First, we multiply exponents to have only one

`(5^{(3)/(4) } )^{(2)/(3) }=(5)^{(3 * 2)/(4 * 3) }=(5)^{(6)/(12) }=5^{(1)/(2) }`

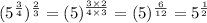
Then, we apply the property to rewrite the expression

`5^{(1)/(2) } =√(5)`

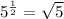
Therefore, the right answer is the third choice.