Question

The eyes of certain reptiles pass a single visual signal to the brain when the visual receptors are struck by photons of a wavelength of 850 nm. If a total energy of 3.15 × 10−14 J is required to trip the signal, what is the minimum number of photons that must strike the receptor?

Answer 1

`n=1.34* 10^5`

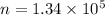
Step-by-step explanation:

It is given that,

Wavelength of the photon,
`\lambda=850\ nm=850* 10^(-9)\ m`

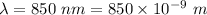
Total energy required to trip the signal,
`E=3.15* 10^(-14)\ J`

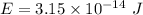
Let n is the minimum number of photons that must strike the receptor. Firsly calculating the energy of one photon as :

`E=(hc)/(\lambda)`

`E=(6.63* 10^(-34)* 3* 10^8)/(850* 10^(-9))`

`E=2.34* 10^(-19)\ J`

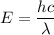
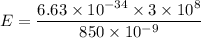
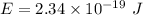
Let n is the number of photons that must strike the receptor. It can be calculated as :

`n=(3.15* 10^(-14))/(2.34* 10^(-19))`

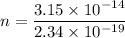
n = 134615.38

or

`n=1.34* 10^5`

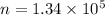
So,
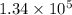`1.34* 10^5` number of photons that must strike the receptor. Hence, this is the required solution.