Question

A 176 inch pole is leaning up against a wall, but is sliding down the wall so that the vertical distance between the top of the pole and the floor is decreasing at a rate of 4 inches per second. How fast is the horizontal distance between the bottom of the pole and the base of the wall changing when the vertical distance is 7 inches? (Do not include units in your answer, and round to the nearest hundredth.)

Answer 1

0.16 inches per second

Explanation:

The vertical height of the pole in inches can be modeled at time t by the expression y=7-4t. The horizontal distance of the end from the wall can be found using the Pythagorean theorem. We want the derivative of that horizontal distance at t=0.

Setup

x² +y² = 176² . . . . . . Pythagorean relation

x² = 176² -y² = 176² -(7 -4t)² . . . . . . substitute time function for y

x² = 30976 -(49 -56t +16t²) . . . . . . expand

x = √(30927 +56t -16t²) . . . . . . . . . square root

Solution

The rate of change of x, the distance of the end from the wall, is the derivative of x with respect to t:

`x'=(56-32t)/(2√(30927+56t-16t^2))`

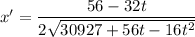
At t=0, this is ...

x'(0) = 28/√30927 ≈ 0.159217

The bottom of the pole is moving away from the wall at the rate of 0.16 inches per second.