Question

In order to calculate the weight of an object sitting on the Earth’s surface, one would use the following formula: FG = GMEm r 2 where G = 6.674 × 10−11 m3 kg s2 is the universal gravitational constant, ME = 5.97 × 1024 kg is the mass of the Earth (also a constant), r is the radius of the Earth at the object’s location (measured in m), and m = the mass of the object (measured in kg). Calculate your weight (to the correct number of significant figures) using this formula if your mass is 9.01 × 104 g and the radius of the Earth at the object’s location is 6.382 × 106 m. Use unit algebra to express the unit for weight as some combination of the metric system’s standard units for mass, length, and time.

Answer 1

The weight is 881.397 N

Step-by-step explanation:

You have to replace the values of G, ME, r and m in the given formula to calculate the weight

`FG=(GMEm)/(r^(2) )`

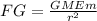
The mass of the object (in this case, your mass) should be replaced in kg, so you have to covert it to kg

Is known that 1000g=1kg, so dividing the mass by 1000 you will obtain the mass is kg:

m =
`((9.01)(10^(4)) )/(1000) = 90.1 kg`

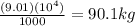
Replacing the values in the formula:

`FG= ((6.674)(10^(-11))(5.97)(10^(24))(90.1)  )/([(6.382)(10^(6) )]^(2) )`

Calculating the value of FG:

FG= 881.397

Now you have to use unit algebra to find the unit for weight. You have to replace just the units in the given formula:

FG=
`((m^(3)/kgs^(2))(kg)(kg))/(m^(2)) = ((m^(3)/kgs^(2))(kg^(2)))/(m^(2) )`

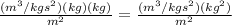
Applying properties of exponential numbers and rational numbers:

`(m^(3)kg^(2))/(kgs^(2)m^(2)) = (kg m)/(s^(2) ) = N`

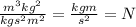
where N is newton, the unit for force.

So, the weight (given by FG) is: 881.397 N