Answer:
Part a)
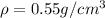
Part b)
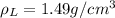
Part c)
Since we know that the base area will remain same always
so here the length and width of the object is not necessary to obtain the above data in such type of questions
Step-by-step explanation:
Part a)
As we know that when cylinder float in the water then weight of the cylinder is counter balanced by the buoyancy force
So here we know
buoyancy force is given as
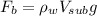
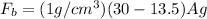
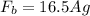
Now we know that the weight of the cylinder is given as
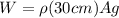
now we have
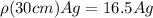
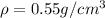
Part b)
When the same cylinder is floating in other liquid then we will have
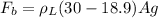
so we have
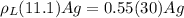
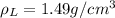
Part c)
Since we know that the base area will remain same always
so here the length and width of the object is not necessary to obtain the above data in such type of questions