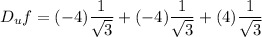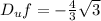Question

Consider the function f (x comma y comma z )equals 1 plus 4 xyz​, the point P(negative 1 comma negative 1 comma 1 )​, and the unit vector Bold uequalsleft angle StartFraction 1 Over StartRoot 3 EndRoot EndFraction comma StartFraction 1 Over StartRoot 3 EndRoot EndFraction comma StartFraction 1 Over StartRoot 3 EndRoot EndFraction right angle . a. Compute the gradient of f and evaluate it at P. b. Find the unit vector in the direction of maximum increase of f at P. c. Find the rate of change of the function in the direction of maximum increase at P. d. Find the directional derivative at P in the direction of the given vector.

Answer 1

This is pretty hard to decipher.

Consider the function f (x comma y comma z )equals 1 plus 4 xyz​,

`f(x,y,z)=1 +4xyz`

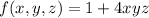
the point P(negative 1 comma negative 1 comma 1 )​,

P(-1, -1, 1)

and the unit vector Bold uequalsleft angle StartFraction 1 Over StartRoot 3 EndRoot EndFraction comma StartFraction 1 Over StartRoot 3 EndRoot EndFraction comma StartFraction 1 Over StartRoot 3 EndRoot EndFraction right angle .

Huh? Oh, I see. We won't stress about the vector notation.

`u =\left((1)/(√(3)),(1)/(√(3)),(1)/(√(3)) \right)`

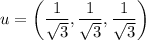
a. Compute the gradient of f and evaluate it at P.

`\\abla f = \left((\partial f)/(\partial x), (\partial f)/(\partial y), (\partial f)/(\partial z) \right)`

`\\abla f = (4yz, 4xz, 4xy)`

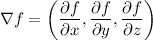
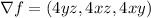
P(-1, -1, 1)

`g =(-4, -4, 4)`

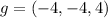
b. Find the unit vector in the direction of maximum increase of f at P.

That's just the normalized version of the above. It has a magnitude

`√(3(4)^2) = 4√(3)`

so we have to divide 4 by that, so 1/√3.

The unit direction vector is

`g =\left( -(1)/(√(3)), -(1)/(√(3)),(1)/(√(3))\right)`

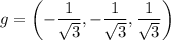
Sometimes they seek the teacher friendly

`g =\left( (-√(3))/(3), -(√(3))/(3), (√(3))/(3) \right)`

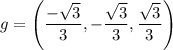
c. Find the rate of change of the function in the direction of maximum increase at P.

We already did, that's the magnitude of the gradient,

`4√(3)`

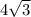
d. Find the directional derivative at P in the direction of the given vector.

We want the total derivative in the direction of u, so that's the weighted average of the partials. For unit direction u=(a,b,c) we can write it

`D_u f = D_((a,b,c)) f =(\partial f)/(\partial z) a + (\partial f)/(\partial z) b + (\partial f)/(\partial z) c`

For us that's

`D_u f = (-4) (1)/(√(3)) + (-4) (1)/(√(3))+(4)(1)/(√(3))`

`D_u f =-\frac 4 3 √(3)`