Question

A single force acts on a 2.0 kg particle-like object in such a way that the position of the object as a function of time is given by x = 3.0t − 4.0t 2 + 1.0t 3, with x in meters and t in seconds. Find the work done on the object by the force from t = 0 to t = 5.0 s.

Answer 1

The work done by the force is 1435 Joule.

Step-by-step explanation:

You have to apply the work-energy theorem, which associates the work and the mechanical energy

W of all non conservative forces = ΔEm = Emb - Ema

where Emb is the mechanical energy in point b and Ema is the mechanical energy in point a

Is also known that mechanical energy is the sum of potential energy and kinetic energy.

In this case, there is only kinetic energy because the potential energy is given by conservative forces like the weight but the weight is perpendicular to the displacement and because of that it doesn't produce work.

So, the work is given by:

W= Ekb - Eka, where Ek is the kinetic energy

By definition the kinetic energy is given by:

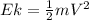`Ek=(1)/(2)mV^(2)` where m is the mass and V is the speed.

Replacing the definition of Ek in the equation of work:

`W=(1)/(2)mVb^(2) - (1)/(2)mVa^(2)`

So, you have to calculate the speed in point a and in point b

You can calculate the velocity of the object as a function of time derivating the equation of the position:

`V(t) = (dX(t))/(dt) = (d(3.0t-4.0t^(2)+1.0t^(3))  )/(dt)`

`V(t)=3.0-8.0t+3.0t^(2)`

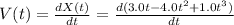
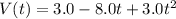
Replacing t=0 s to obtain the speed in the initial point (point a)

Va=3.0-8(0)+3.0(0)(0)

Va=3.0 m/s

Replacing t=5.0 to obtaing the speed in final point (point b)

Vb= 3-8(5)+3(5)(5) = 38 m/s

Therefore the work is:

`W = (1)/(2)(2.0)(38)^(2) - (1)/(2)(2.0)(3^(2)) =1444 - 9 = 1435 [J]`

Where J is Joules, the unit for work.