ANSWER:
The factors of the expression
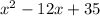 are (x – 7) and (x – 5).
are (x – 7) and (x – 5).
SOLUTION:
Given, Trinomial expression is
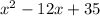
Trinomial is nothing but an expression or equation having three terms in it.
Given expression is quadratic expression.
Now, to factorize any quadratic expression we need to write the constant term as product of two numbers, such that sum two number should equal to coefficient of x, in order to take common.

By writing constant as product of two numbers, we get

By writing the “x” term as sum of two number coefficients, we get
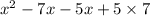
By taking x and -5 as common
x(x – 7) –5(x – 7)
By taking (x – 7) as common, the above expression becomes,
(x – 7)(x – 5)
Thus factors of the expression
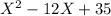 are (x – 7) and (x – 5).
are (x – 7) and (x – 5).