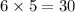Question

Amy is choosing a 2-letter password from the letters A, B, C, D, E, and F. The password cannot have the same letter repeated in it. How many such passwords are possible?

Answer 1

30

Explanation:

6 choices for the 1st, then 5 choices for the 2nd, so: 6*5=30

or nPk=n!/(n-k)! with n=6 and k=2

Put it simply each letter can be combined with 5 diffrent letters and with 6 total letters 6x5=30

Answer 2

Amy can choose from 60 possible passwords.

Solution:

Given that the two-letter password is from the letters A, B, C, D, E and F

Total number of letters = 6

The password is a two digit letter and repetition of letters is not allowed.

Method 1:

\therefore The number of ways of obtaining an ordered subset of r elements from a set of n elements is given by

`^(n) P_(r) = (n!)/((n-r)!)`

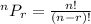
So, the total possible password =
`^(6)P_(r) = (6!)/((6-4)!)` =
`(6!)/(4!)` =
`(6*5*4!)/(4!)`

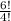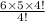
On cancelling the
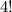`4!` in numerator and denominator we get,

Here we get,
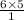`(6*5)/(1)` = 30 possible passwords

Method 2:

There are 6 possible choices for the first term of the password and 5 choices for the second term (i.e. leaving the selected letter of the
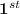`\bold1^(st)\bold` term)

So,
`6* 5 = 30`