Question

Given that the length an athlete throws a hammer is a normal random variable with mean 50 feet and standard deviation 5 feet, what is the probability he throws it between 50 feet and 60 feet?

Answer 1

The probability he throws it between 50 feet and 60 feet is 0.48

Explanation:

* Lets revise how to find the z-score

- The rule the z-score is z = (x - μ)/σ , where

# x is the score

# μ is the mean

# σ is the standard deviation

* Lets solve the problem

- The mean is 50 feet

- The standard deviation 5 feet

- We need to find the probability of his throws between 50 feet and

60 feet

∵ z = (x - μ)/σ

∵ x = 50 and 60

∵ μ = 50

∵ σ = 5

- Substitute these values in the rule above

∴ z =
`(50-50)/(5)`

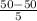
∴ z = 0

∴ z =
`(60-50)/(5)`

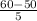
∴ z = 2

- Lets use the normal distribution table of z to find the corresponding

area to z score

∵ P(z > 0) = 0.5

∵ P(z < 2) = 0.97725

- Subtract the two areas

∴ P(0 < z < 2) = 0.97725 - 0.5 = 0.47725

∵ P(50 < x < 60) = P(0 < z < 2)

∴ P(50 < x < 60) = 0.47725

∴ P(50 < x < 60) ≅ 0.48

The probability he throws it between 50 feet and 60 feet is 0.48