Question

Given that A ( 5, 4), B(-3, -2 ) and C(1, -8) are the vertices of a triangle ABC,

find the slope of altitude BM

Answer 1

The slope of the altitude BM is
`(1)/(3)`

Solution:

Given that A(5,4), B(-3,-2) and C(1,-8) are the vertices of a triangle ABC . We have to find the slope of altitude BM

The figure of the given question is given below. Here M is the mid-point of side AC.

To find the slope of altitude BM, we need to first find the slope of AC.

The slope of AC is given by

`(y_(2)-y_(1))/(x_(2)-x_(1))` ---- eqn 1

Given that points of A(5,4) and C(1,-8)

Here we get
`y_(2)=-8`

`y_(1)=4`

`x_(2)=1`

`x_(1)=5`

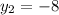
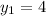
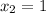
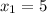
Now substituting the values in eqn (1), we get

`\text { Slope of } \mathrm{AC}=(-8-4)/(1-5)`

`=(-12)/(-4)`

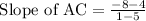
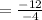
= 3

The slope of the Altitude BM is given by the reciprocal of the slope of AC since M is the midpoint of AC.

`\text { Slope of } \mathrm{BM}=\frac{1}{\text { slope of } A C}`

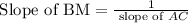
Slope of BM =
`(1)/(3)`

Thus the slope of the altitude BM is
`(1)/(3)`