Question

One strategy in a snowball fight is to throw

a snowball at a high angle over level ground.
While your opponent is watching this first
snowball, you throw a second snowball at a
low angle and time it to arrive at the same
time as the first.
Assume both snowballs are thrown with
the same initial speed 20.5 m/s. The first
snowball is thrown at an angle of 68◦
above
the horizontal. At what angle should you
throw the second snowball to make it hit the
same point as the first? The acceleration of
gravity is 9.8 m/s

The answer is: 22

Part 2:
How many seconds after the first snowball
should you throw the second so that they
arrive on target at the same time?
Answer in units of s.
PLEASE FIND OUT PART 2

Answer 1

Part One:
`22^(\circ)`;

Part Two: Toss the snowball approximately
`2.31` seconds after tossing the first snowball.

Assumption: there's no air resistance on the snowballs. Both snowballs stay intact during the flight.

Step-by-step explanation:

Part One

• Initial vertical velocity of the first snowball:
  `20.5\sin 68^(\circ) \approx \rm 19.0\; m\cdot s^(-1)`;
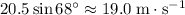• Horizontal velocity of the first snowball:
  `20.5\cos68^(\circ) \approx \rm 7.68\;m \cdot s^(-1)`.

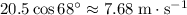How long will the first snowball stay in the air?

• The ball reaches its vertex (highest point in the trajectory, where vertical velocity is zero) at
  `\displaystyle ( 19.0)/(9.81)\; \rm s`.
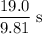• It will take the ball another
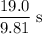  `\displaystyle ( 19.0)/(9.81)\; \rm s` to land. In other words, the first snowball stays in the air for
  `\displaystyle 2* ( 19.0)/(9.81)\; \approx 3.97\rm s`.

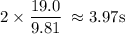What will be the range of the first snowball? In other words, how far will the first ball travel horizontally before it lands?

`3.97 * 7.68 \approx 30.5\; \rm m`.

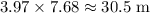That should also be the range of the second snowball.

Let the angle of elevation of the second snowball at takeoff be
`\theta`.

• Initial vertical velocity of the second snowball:
  `20.5\sin \theta`;
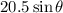• Horizontal velocity of the second snowball:
  `20.5\cos\theta`.

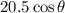The second snowball will spend

`\displaystyle (30.5)/(20.5\cos\theta)` seconds

in the air before covering that range of approximately
`30.5\; \rm m`.

It would take half that much time for the ball to reach its vertex where its vertical velocity equals zero.

`\displaystyle (20.5\sin \theta)/(9.8) = (1)/(2)\cdot(30.5)/(20.5\cos\theta)`.

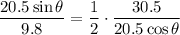Solve this equation for the angle
`\theta`.

Multiply both sides by
`2* 9.8* 20.5\cos\theta`:

`20.5^(2)(2\sin\theta \cos\theta)= 30.5* 9.8`.

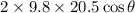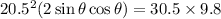Apply the double-angle identity for the sine of an angle:

`2\sin\theta \cos\theta = \sin 2\theta`:

`20.5^(2) \sin2\theta= 30.5* 9.8`.

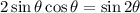The result shall be between
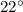`22^\circ` and
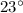`23^\circ`. For a more precise value, keep more significant figures during the calculation.

Part Two

Recall that it is concluded in part one that the second snowball will spend

`\displaystyle (30.5)/(20.5\cos\theta)` seconds

in the air before covering that range of approximately
`30.5\; \rm m` (or more precisely,
`29.7888\rm \; m`.)

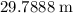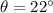`\theta = 22^\circ`. The second snowball will spend
`\displaystyle (29.7888)/(20.5\cos22^(\circ))\approx 1.5672\; \rm s` in the air.

The first snowball will spend around
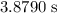`3.8790\rm \; s`. The difference between the two time is the number of seconds that the person throwing the snowball need to wait:

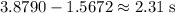`3.8790 - 1.5672 \approx 2.31\rm \; s`.