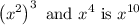Question

What is the product of (x2)3 and x4 ?

Answer 1

the answer is x24. work is show in the drawing .

Answer 2

The product of given two terms
`\left(x^(2)\right)^(3) \text { and } x^(4) \text { is } x^(10)`

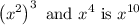
SOLUTION:

Given, two terms are
`\left(x^(2)\right)^(3) \text { and } x^(4)`

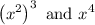
First term is in indirect form, so let us convert it into direct form first.

we know the identity
`\left(a^(m)\right)^(n)=a^(m * n)`

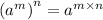
applying this identity in above expression,
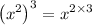`\left(x^(2)\right)^(3)=x^(2 * 3)`becomes,

`\left(x^(2)\right)^(3)=x^(6)`

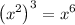
As the the second term is in direct form, we can now multiply both the terms.

Now, product of two terms =
`x^(6) * x^(4)`

we know the identity
`a^(m) * a^(n)=a^(m+n)`

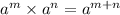
when exponential terms with same base are multiplied, power should be added. So we get
`X^(6+4)`

`X^(6+4)=X^(10)`

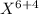
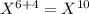
Hence the product of two terms
`\left(x^(2)\right)^(3) \text { and } x^(4) \text { is } x^(10)`