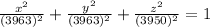Question

Because of the forces caused by its rotation, Earth is an oblate ellipsoid rather than a sphere. The equatorial radius is 3963 miles and the polar radius is 3950 miles. Find an equation of the ellipsoid. (Assume that the center of Earth is at the origin and that the trace formed by the plane z = 0 corresponds to the equator.)

Answer 1

The required equation of the ellipsoid is:

`(x^2)/((3963)^2)+(y^2)/((3963)^2)+(z^2)/((3950)^2)=1`

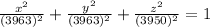
Explanation:

Consider the provided information.

The standard equation of ellipsoid is:

`(x^2)/(a^2)+(y^2)/(b^2)+(z^2)/(c^2)=1`

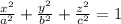
The equatorial radius is 3963 miles and the polar radius is 3950 miles. Also the trace formed by z = 0 corresponds to equator.

Here the equatorial radius is 3963 miles and trace formed by z = 0.

It is also given that the polar radius is 3950, that represents the distance on z axis, so substitute a=3963, b=3963 and c=3950 in the above equation.

The required equation of the ellipsoid is:

`(x^2)/((3963)^2)+(y^2)/((3963)^2)+(z^2)/((3950)^2)=1`