Answer:
Perimeter of rectangle=

=
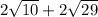 .
.
Explanation:
Given:
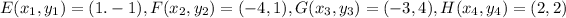
Using distance formula:
Length of EF =
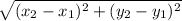
=
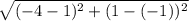
=
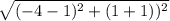
=
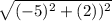
=

=
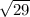
Length of FG =
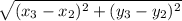
=
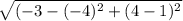
=
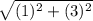
=
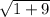
=
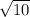
Length of GH =

=
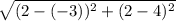
=
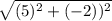
=

=
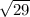
Length of HE =
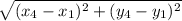
=
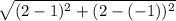
=
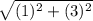
=
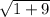
=
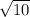
∵ EFGH is a rectangle ∴ EH = FG and EF = HG
Perimeter of rectangle = 2 ( EF + FG + GH + HE)
= 2 (EF + FG)
=

=
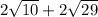
Therefore option (b) is the correct answer.