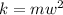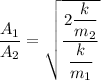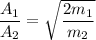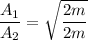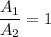Answer:
Step-by-step explanation:
given,
two identical spring have identical spring constant
mass 'm' is hanging on one spring and mass of '2m' on another wall.
energy of the two system is same
energy of the system having mass 'm'
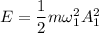
energy of the system having mass '2m'
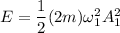
now, Energy are same
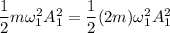
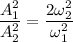
we know