Answer:
$ 127,773.36
Step-by-step explanation:
The professor will be in sabbatical in years 7, 14, 21, 28, 35 and 42
In each of these years, he receives full pay amounting to=50,000
The PV of the sabbatical full pay
=
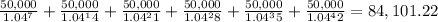
=50,000/(1+4%)^7+ 50,000/(1+4%)^14+ 50,000/(1+4%)^21+ 50,000/(1+4%)^28+50,000
/(1+4%)^35+ 50,000/(1+4%)^42
==50,000/(1+4%)^7+ 50,000/(1+4%)^14+ 50,000/(1+4%)^21+ 50,000/(1+4%)^28+50,000
/(1+4%)^35+ 50,000/(1+4%)^42
=
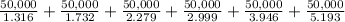
=37,993.92 + 28,868.36 + 21,939.45 + 16,672.22 + 12,671.06 + 9,628.35
= $ 127,773.36
Thus, at an interest rate of 4%, the present value of all the sabbatical earnings amount to $ 127,773.36