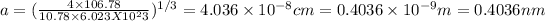Answer:
The edge length is 0.4036 nm
Solution:
As per the question:
Density of Ag,
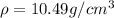
Density of Pd,
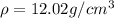
Atomic weight of Ag, A = 107.87 g/mol
Atomic weight of Pd, A' = 106.4 g/mol
Now,
The average density,
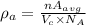
where
 = Volume of crystal lattice
= Volume of crystal lattice
a = edge length
n = 4 = no. of atoms in FCC
Therefore,
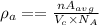
Therefore, the length of the unit cell is given as:
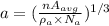 (1)
(1)
Average atomic weight is given as:
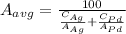
where
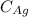 = 79 %
= 79 %
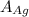 = 107
= 107
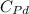 = 21%
= 21%
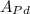 = 106
= 106
Therefore,
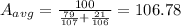
In the similar way, average density is given as:
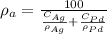
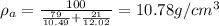
Therefore, edge length is given by eqn (1) as: