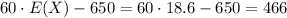Answer:
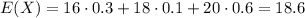
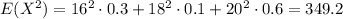
![V(X) = E(X^2)-[E(X)]^2=349.2-(18.6)^2=3.24](https://img.qammunity.org/2020/formulas/mathematics/college/27kh0oinima6jpbg1oluggj0h8hi5w8ljk.png)
The expected price paid by the next customer to buy a freezer is $466
Explanation:
From the information given we know the probability mass function (pmf) of random variable X.
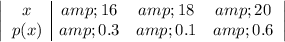
Point a:
- The Expected value or the mean value of X with set of possible values D, denoted by E(X) or μ is
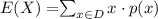
Therefore
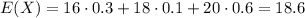
- If the random variable X has a set of possible values D and a probability mass function, then the expected value of any function h(X), denoted by E[h(X)] is computed by
![E[h(X)] = $\sum_(D) h(x)\cdot p(x)](https://img.qammunity.org/2020/formulas/mathematics/college/r5ba35kjio0t22dg1v8z5599xia37ysaab.png)
So
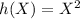 and
and
![E[h(X)] = $\sum_(D) h(x)\cdot p(x)\\E[X^2]=$\sum_(D)x^2\cdot p(x)\\ E(X^2)=16^2\cdot 0.3+18^2\cdot 0.1+20^2\cdot 0.6\\E(X^2)=349.2](https://img.qammunity.org/2020/formulas/mathematics/college/dotg73b0r4w1cg1005fshpbkmb5dwiv168.png)
- The variance of X, denoted by V(X), is
![V(X) = $\sum_(D)E[(X-\mu)^2]=E(X^2)-[E(X)]^2](https://img.qammunity.org/2020/formulas/mathematics/college/noi90rrxphiflmdzswyr09px634r2o9g7u.png)
Therefore
![V(X) = E(X^2)-[E(X)]^2\\V(X)=349.2-(18.6)^2\\V(X)=3.24](https://img.qammunity.org/2020/formulas/mathematics/college/kqorh2rhemfos7iht8fj47oitzm1djy0ng.png)
Point b:
We know that the price of a freezer having capacity X is 60X − 650, to find the expected price paid by the next customer to buy a freezer you need to:
From the rules of expected value this proposition is true:
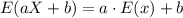
We have a = 60, b = -650, and E(X) = 18.6. Therefore
The expected price paid by the next customer is