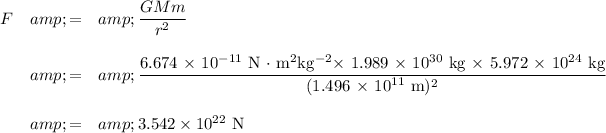Answer:
(a) 5.91 × 10⁸ N; (b) 3.542 × 10²² N
Step-by-step explanation:
Data:
I = 1.39 kW/m² = 1.39 × 10³ N·m⁻³s⁻¹
c = 2.998 × 10⁸ m/s
r = 6370 km = 6.37 × 10⁶ m
G = 6.674 ×10⁻¹¹ N⋅m²kg⁻²
M = 1.989 × 10³⁰ kg = mass of Sun
m = 5.972 × 10²⁴ kg = mass of Earth
d = 1.496 × 10¹¹ m = distance from Earth to Sun
Calculations:
(a) Force exerted by the radiation pressure
(i) Radiation pressure
All the incident radiation is absorbed, so
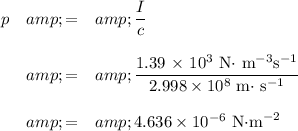
(ii) Area of Earth's disc
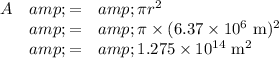
(iii) Radiation force
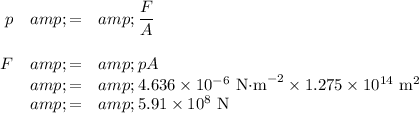
(b) Gravitational Force