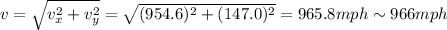Question

A jet airliner moving initially at 406 mph (with respect to the ground) to the east moves into a region where the wind is blowing at 568 mph in a direction 15◦ north of east. What is the new speed of the aircraft with respect to the ground?

Answer 1

966 mph

Step-by-step explanation:

Using as convention:

- East --> positive x-direction

- North --> Positive y-direction

The x- and y- components of the initial velocity of the jet can be written as

`v_(1x) = 406 mph\\v_(1y) = 0`

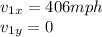
While the components of the velocity of the wind are

`v_(2x) = (568)(cos 15^(\circ))=548.6 mph\\v_(2y) = (568)(sin 15^(\circ))=147.0 mph`

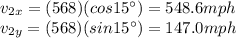
So the components of the resultant velocity of the jet are

`v_x = v_(1x)+v_(2x)=406+548.6=954.6 mph\\v_y = v_(1y)+v_(2y)=0+147.0=147.0 mph`

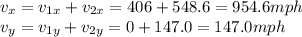
And the new speed is the magnitude of the resultant velocity:

`v=√(v_x^2+v_y^2)=√((954.6)^2+(147.0)^2)=965.8 mph \sim 966 mph`