Answer:
The deuterium will have a larger radius of curvature, since it is more massive.
Step-by-step explanation:
Suppose that the initial velocity of deuterium and protons is the same. According to the relation for centripetal acceleration:
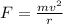
The force is the same due to same electric charge between proton and deuterium. Solving for r:
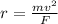
It means that, the more the mass, the larger the radius due to the directly proportional relation.