Answer:
a)
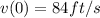
b)
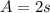
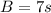
c)
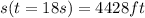
d) Δs=4428ft
Step-by-step explanation:
From the exercise we know the equation of position

a) To calculate the velocity we need to derivate the equation of position
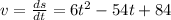
So, v(0) is:
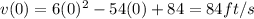
b) To find the two times where the particle stops A and B we need to solve the quadratic equation:
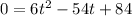
Solving for t
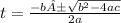
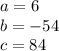
 and
and
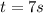
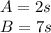
c)

d) Δs=4428ft-0ft=4428ft