Question

H2SO4 is an unusual diprotic acid in that the first dissociation is considered strong, but the second dissociation is weak. Therefore, H2SO4 only has Ka2 = 1.2x10−2. Consider an aqueous solution containing 0.010 M H2SO4. Calculate the concentration of SO42− ions in this solution. Calculate the concentration of HSO4− ions in this solution. Calculate the concentration of H3O+ ions the solution. Enter each of your answers to two significant figures. Do not use scientific notation.

Answer 1

Step-by-step explanation:

As it is given that the initial concentration of sulfuric acid is 0.010 M.

Hence, the ICE table for first dissociation of sulfuric acid is as follows.

`H_(2)SO_(4) + H_(2)O \rightleftharpoons HSO^(-)_(4) + H_(3)O^(+)`

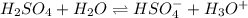
Initial: 0.010 0 0

Change: -0.010 +0.010 +0.010

Equilibrium: 0 0.010 0.010

When second dissociation of sulfuric acid occurs which is partial then the ICE table will be as follows.

`HSO^(-)_(4) + H_(2)O \rightleftharpoons SO^(2-)_(4) + H_(3)O^(+)`

Initial: 0.010 0 0.010

Change: -x +x +x

Equilibrium: 0.010 - x x 0.010 + x

Since, it is given that
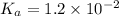`K_(a) = 1.2 * 10^(-2)`. Hence, formula for
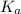`K_(a)` is as follows.

`K_(a) = ([SO^(2-)_(4)][H_(3)O^(+)])/([HSO^(-)_(4)])`

`1.2 * 10^(-2) = (x(0.010 + x))/((0.010 - x))`

`0.0012 * (0.010 - x) = x(0.010 + x)`

`0.00012 - 0.012x = x^(2) + 0.010x`

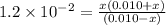
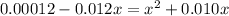
x = 0.0045

Hence, by using the equilibrium concentrations from the table and value of x we get the following.

• 
  `[SO^(2-)_(4)]` = x,

= 0.0045 M

• 
  `[HSO^(-)_(4)]` = 0.010 - x

= 0.010 - 0.0045

= 0.0055 M

• 
  `[H_(3)O^(+)]` = 0.010 + x

= 0.010 + 0.0045

= 0.0145 M