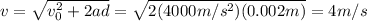Answer:
v=4m/s
Step-by-step explanation:
The formulas for accelerated motion are:
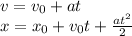
We can derive the formula
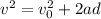 from them.
from them.
We have:
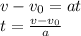
And substitute:
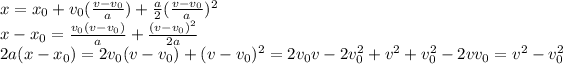
Where in the first step of the last row we just multiplied everything by 2a. Since
 is the displacement d, we have proved that
is the displacement d, we have proved that
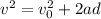
We use then our values to calculate the final velocity when starting from rest, traveling a distance 0.002m with acceleration
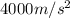 :
: