Question

The Better Baby Buggy Co. has just come out with a new model, the Turbo. The market research department predicts that the demand equation for Turbos is given by 

q = −4p + 544,

 where q is the number of buggies the company can sell in a month if the price is $p per buggy. At what price should it sell the buggies to get the largest revenue?

Answer 1

$68

Explanation:

We have been given the demand equation for Turbos as
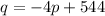`q=-4p+544`, where q is the number of buggies the company can sell in a month if the price is $p per buggy.

Let us find revenue function by multiplying price of p units by demand function as:

Revenue function:
`pq=p(-4p+544)`

`pq=-4p^2+544p`

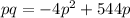
Since revenue function is a downward opening parabola, so its maximum point will be vertex.

Let us find x-coordinate of vertex using formula
`(-b)/(2a)`.

`(-b)/(2a)=(-544)/(2* -4)`

`(-b)/(2a)=(-544)/(-8)`

`(-b)/(2a)=68`

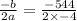
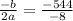
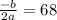
The maximum revenue would be the y-coordinate of vertex.

Let us substitute
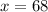`x=68` in revenue formula.

`pq=-4(68)^2+544(68)`

`pq=-4*4624+544(68)`

`pq=-18496+36992`

`pq=18496`

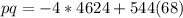
Therefore, the company should sell each buggy for $68 to get the maximum revenue of $18,496.