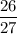Question

To avoid detection at customs, a traveler places 6 narcotic tablets in a bottle containing 9 vitamin tablets that are similar in appearance. If the customs official selects 3 of the tablets at random for analysis, what is the probability that the traveler will be arrested for illegal possession of narcotics?

Answer 1

Answer:
`(26)/(27)`

Explanation:

Given : To avoid detection at customs, a traveler places 6 narcotic tablets in a bottle containing 9 vitamin tablets that are similar in appearance.

Proportion of success :
`p=(6)/(9)=(2)/(3)`

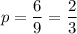
Sample size taken by customs official : n= 3

Let x be a binomial variable that represents the tablets in the bottle.

Using Binomial probability formula :-

`P(X=x)=^nC_xp^x(1-p)^(n-x)`

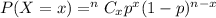
The probability that the traveler will be arrested for illegal possession of narcotics =
`P(x\geq1)=1-P(x=0)`

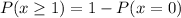
`1-^3C_0((2)/(3))^0(1-(2)/(3))^3\\\\=1-(1)(1)((1)/(3))^3\ [\becuase ^nC_0=1]\\\\=1-(1)/(27)=(26)/(27)`

Hence, the probability that the traveler will be arrested for illegal possession of narcotics =
`(26)/(27)`