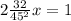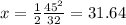Answer:
31.64 feet
Explanation:
The height is given by the equation:
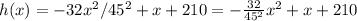
where x is the horizontal distance of the projectile from the face of the cliff.
If the height is maximum, then its derivative must be h'(x)=0. Remembering that the derivative of
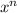 is
is
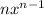 , we have:
, we have:
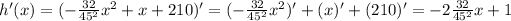
And we want h'(x)=0, so:
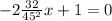
This will give us the horizontal distance from the face of the cliff when the height of the projectile is at its maximum. We then do: