Question

At a specific point on a highway, vehicles arrive according to a Poisson process. Vehicles are counted in 12 second intervals, and vehicle counts are taken in 120 of these time intervals. No cars arrive in 15 of these 120 intervals. a. Approximate the number of these intervals in which exactly one car arrives. (1 point) b. Estimate the percentage of time headways that will be 14 seconds or greater. (1 point) Hint: use t=14 seconds and x=0

Answer 1

Answer: a) 4.6798, and b) 19.8%.

Explanation:

Since we have given that

P(n) =
`(15)/(120)=0.125`

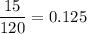
As we know the poisson process, we get that

`P(n)=((\lambda t)^n* e^(-\lambda t))/(n!)\\\\P(n=0)=0.125=((\lambda * 14)^0* e^(-14\lambda))/(0!)\\\\0.125=e^(-14\lambda)\\\\\ln 0.125=-14\lambda\\\\-2.079=-14\lambda\\\\\lambda=(2.079)/(14)\\\\0.1485=\lambda`

So, for exactly one car would be

P(n=1) is given by

`=((0.1485* 14)^1* e^(-0.1485* 14))/(1!)\\\\=0.2599`

Hence, our required probability is 0.2599.

a. Approximate the number of these intervals in which exactly one car arrives

Number of these intervals in which exactly one car arrives is given by

`0.2599* 18=4.6798`

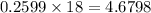
We will find the traffic flow q such that

`P(0)=e^{(-qt)/(3600)}\\\\0.125=e^{(-18q)/(3600)}\\\\0.125=e^(-0.005q)\\\\\ln 0.125=-0.005q\\\\-2.079=-0.005q\\\\q=(-2.079)/(-0.005)=415.88\ veh/hr`

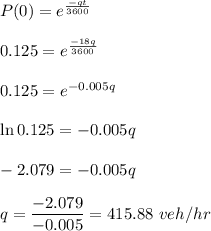
b. Estimate the percentage of time headways that will be 14 seconds or greater.

so, it becomes,

`P(h\geq 14)=e^{(-qt)/(3600)}\\\\P(h\geq 14)=e^{(-415.88* 14)/(3600)}\\\\P(h\geq 14)=0.198\\\\P(h\geq 14)=19.8\%`

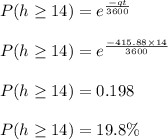
Hence, a) 4.6798, and b) 19.8%.